Мощным побудительным стимулом явилась для него так называемая теорема Ферма о сравнении атº1 (mod p), значение которой он оценил сразу. Эйлеру принадлежат два доказательства этой теоремы, покоящихся на разных основаниях. Первое [Comm. Ac. Petr., 1736(1741)] использовало тот факт, что все биномиальные коэффициенты, соответствующие показателю степени р, делятся на р, и было проведено с помощью индукции. Второе и третье доказательства появились в Nov. Comm. Ac. Petr. за 1758/59 (1761) и 1760/61 (1763).

В последней статье Эйлер обобщил теорему Ферма, установив (в обозначениях, ведущих свое происхождение от Гаусса), что

аj(m) º 1 (mod m),

где j(т) есть число чисел, взаимно простых с т и меньших т. Встречающееся здесь число j(т), которое по предложению Гаусса называют теперь «функцией Эйлера», последний представил в той же работе в виде

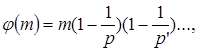
где р, р’, . — простые делители числа т. Если т само есть простое число, то числа 1, 2, 3, ., (р - 1) будут с ним взаимно простыми, и получается важная теорема, высказанная Дж. Вильсоном и опубликованная в 1770 Варингом в его «Алгебраических размышлениях». Теорема эта гласит, что величина 1, 2, 3 . (р - 1)+1 делится без остатка на р, где р, как и всюду здесь, — простое число. Эта теорема, как и теорема Ферма, заключается в установленном Лагранжем [Mem. Ac. Bed., 1771 (1773)] общем сравнении

xp-l - l=(x + l)(x + 2) .(x+p - 1) (mod р)

при x = 0. Она была также доказана Эйлером («Аналитические сочинения», I, 1783) и Гауссом («Арифметические исследования», 1801). Упрощенное доказательство теоремы Ферма дал еще И. Г. Ламберт, охотно занимавшийся и теорией чисел (Nov. Acta Erud., 1769).

§4.3. Вычеты

К важнейшим достижениям в исследовании целых чисел Эйлера привели старания доказать другую, упоминавшуюся уже, теорему Ферма о том, что всякое простое число вида 4п + 1 разбивается на сумму двух квадратов. Эйлер многократно и с различных сторон подходил к этой теореме и при этом нашел ряд интересных предложений. Окончательно доказать ее Эйлеру удалось лишь в 1749 [Nov. Comm. Ac. Petr., 1754/55 (1760)], воспользовавшись тем ходом мыслей, которым он шел в первом доказательстве теоремы о сравнении ат = 1 (mod р). Это привело его к рассмотрению остатков от деления квадратов 12, 22, 32, ., (р - 1)2 на простое число р. Эйлер немедленно увидел, что при этом получаются «многие замечательные свойства, изучение которых проливает немало света на природу чисел». Таким образом, он впервые поставил вопрос о квадратичных вычетах и понял их значение. Здесь уже встречаются и термины: вычеты (residua) и невычеты, (non residua). В том же месте и в позднейших статьях, в которых он занялся степенными вычетами вообще и рассмотрел полные и неполные системы вычетов, он установил важнейшие относящиеся к ним теоремы. В Nov. Comm. Ac. Petr., 1773 (1774) он ввел также понятие и слово «первообразный корень». Поэтому Эйлера справедливо называют творцом теории степенных вычетов, тем более что ему принадлежит и открытие «закона взаимности» квадратичных вычетов, который Гаусс называл «основной теоремой» (theorema fundamentale) и который до недавнего времени приписывали Лежандру. Закон взаимности Эйлер установил еще в 1772, а опубликован он был, правда, без доказательства, в 1783 в первом томе «Аналитических сочинений».

Октябрьская революция и политика большевиков в первые годы советской власти.
16 октября состоялось расширенное заседание ЦК партии большевиков, на котором было принято решение о подготовке восстания. Воспользовавшись приказами властей о выводе части Петроградского гарнизона на фронт и закрытии большевистской типографии, Л.Д.Троцкий заявил, что началось выступление контрреволюционных сил. Утром 24 октября части В ...

Экономические, политические, мировоззренческие характеристики развития стран Европы в средние века
Хронологические рамки периода средневековой ци­вилизации определяются историками неодинаково. Дол­гое время отечественные исследователи, рассматривая средневековье как время эволюции феодального способа производства, начинали эту эпоху с падения Западной Римской империи (476) и завершали ее началом англий­ской буржуазной революции (1640 ...

Общественно-политическое развитие России в 1991-2004гг.
Демократизация политического режима, начавшаяся в период "перестройки", привела к утверждению в политической системе принципа разделения властей. 21 сентября 1993г президент подписал указ о роспуске съезда народных депутатов и Верховного совета и о проведении поэтапной конституционной реформы. 12 декабря1993г в ходе народного ...